Едсгер Дейкстра - Шлумбергер сентениял професор по компютърни науки и ностител на наградата 'Тюринг'
Едсгер Дейкстра е холандски информатик. През 1972 година той получава наградата "Тюринг” за основополагащите си приноси за развитието на езиците за програмиране. Призът се равнява на Нобелова награда. Дейкст
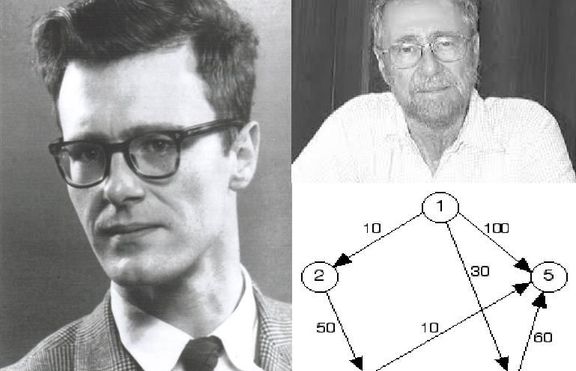
Едсгер Дейкстра е холандски информатик. През 1972 година той получава наградата "Тюринг” за основополагащите си приноси за развитието на езиците за програмиране. Призът се равнява на Нобелова награда. Дейкстра е шлумбергер сентениял професор по компютърни науки в Тексаския университет - Остин от 1984 до 2000 година. След смъртта на Дейкстра, през 2003 година наградата ACM PODC за влиятелни научни публикации върху принципите на разпределените изчислителни системи е прекръстена на Премия Дейкстра.
Дейкстра пръв въвежда термина структурирано програмиране в информатиката. Той е автор на алгоритъма, който носи неговото име.
Алгоритъмът на Дейкстра служи за пресмятане на най-къс път от даден връх до всички останали в ориентиран граф с неотрицателни тегла на ребрата. Може да се модифицира и да се използва за намиране на някои други видове оптимални пътища.
Алгоритъмът намира приложение най-вече в информатиката и логистиката, където често се търси най-късото разстояние между две точки (в програма за GPS устройства, където трябва да се планира най-краткото трасе между стартовата и крайната позиция; оптимизация на транспорта; задача за търговския пътник ... )
Алгоритъмът на Дейкстра, както този на Белман-Форд, използва техниката на релаксация. Първоначално всеки връх има безкрайна дължина, която се намалява при изпълнение на алгоритъма. Алгоритъмът работи, като поддържа дължината на намерения до момента най-кратък път до всеки връх и постепенно разширява множество /S/ от върховете, за които тази дължина със сигурност е оптимална. Алгоритъмът приключва, когато всички върхове на графа са в множеството S.
Коментари 

Вход и регистрация
Влез или се регистрирай за да пишеш...








 2001 - 2025 Всички права запазени.
2001 - 2025 Всички права запазени.